We propose a new representation of visual data that disentangles object position from appearance. Our method, termed Deep Latent Particles (DLP), decomposes the visual input into low-dimensional latent ``particles'', where each particle is described by its spatial location and features of its surrounding region. To drive learning of such representations, we follow a VAE-based approach and introduce a prior for particle positions based on a spatial-softmax architecture, and a modification of the evidence lower bound loss inspired by the Chamfer distance between particles. We demonstrate that our DLP representations are useful for downstream tasks such as unsupervised keypoint (KP) detection, image manipulation, and video prediction for scenes composed of multiple dynamic objects. In addition, we show that our probabilistic interpretation of the problem naturally provides uncertainty estimates for particle locations, which can be used for model selection, among other tasks.

Goal: represent an image as a set of particles, where each particle is described by its spatial location \( z_p = (x,y) \), where \( (x,y) \) are the coordinates of pixels, and latent features \(z_{\alpha} \) that describe the visual features in the surrounding region. $$ \{(z_p^i, z_{\alpha}^i)\}_{i=1}^{K}. $$ Architecture:
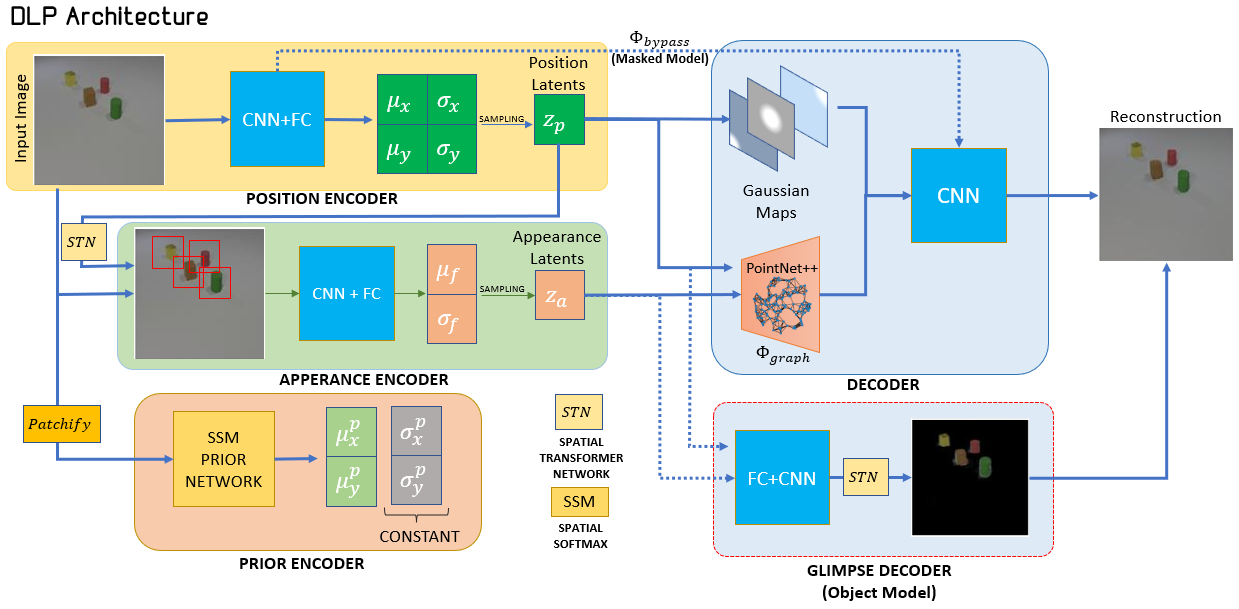
DLP comes in two flavors depending on the scene type: (1) Masked model and (2) Object-based model.

1. Masked model: designed for non-object scenes (e.g., faces from CelebA), PointNet++ and Gaussian maps model the local regions around the particles, and the rest (e.g., the background) is propagated from the encdoer (\(\Phi_{bypass} \)).
2. Object-based model: designed for object-based scenes (e.g., CLEVRER), PointNet++ models the global regions (e.g., the background) and Gaussian maps (optionally) and a separate Glimpse decoder model the objects and their masks.

Architecture - Encoder (Posterior):
The encoder is composed of two components: (1) Position encoder and (2) Appearance encoder.

1. Position encoder: outputs keypoints -- the spatial location \( z_p = (x,y) \) of interesting areas, where \( (x,y) \) are the coordinates of pixels.
2. Appearance encoder: extracts patches (or glimpses) of pre-determined size centered around \( z_p \) and encodes them to latent variables \(z_{\alpha} \).

Architecture - Prior:
The prior addresses the question: what are the interesting areas in the image? Inspired by KeyNet [1], we extract points-of-interest in the image by applying spatial-Softmax (SSM) over feature maps extracted from patches in the image. We term the set of extracted prior keypoints as keypoint proposals.
Architecture - Decoder (Likelihood):
The decoder architecture depends on the scene type as described in the begining.

1. Masked model: PointNet++ and Gaussian maps model the local regions around the particles, and the rest (e.g., the background) is propagated from the encdoer (\(\Phi_{bypass} \)).
2. Object-based model: PointNet++ models the global regions (e.g., the background) and Gaussian maps (optionally) and a separate Glimpse decoder model the objects and their masks.

Architecture - Putting it All Together:

Training and Optimization:
The model is optimized as a variational autoencoder (VAE) with objective of maximizing the evidence lower bound (ELBO): $$ \log p_\theta(x) \geq \mathbb{E}_{q(z|x)} \left[\log p_\theta(x|z)\right] - KL(q(z|x) \Vert p(z)) \doteq ELBO(x) $$ The ELBO is decomposed to the reconstruction error and a KL-divergence regularization term.
However, here we have two unordered sets (or point clouds) of position latent variables: the posterior keypoints and the keypoint proposals from the prior. Note that the number of points in each set may also differ.
Inspired by the Chamfer distance between two sets \( S_1 \) and \( S_2 \): $$ d_{CH}(S_1, S_2) = \sum_{x \in S_1}\min_{y \in S_2}||x-y||_2^2 + \sum_{y \in S_2}\min_{x \in S_1}||x-y||_2^2. $$
Animation by Luke Hawkes [2].
We propose the Chamfer-KL, a novel modification for the KL term: $$ d_{CH-KL}(S_1, S_2) = \sum_{x \in S_1}\min_{y \in S_2}KL(x \Vert y) + \sum_{y \in S_2}\min_{x \in S_1}KL(x \Vert y). $$ Note that the Chamfer-KL is not a metric and maintains the properties of the standard KL term.
Intuitively, the prior proposes interesting locations for keypoints based on SSM and the posterior picks good locations that align with the reconstruction objective, whilst not being limited by the averaging operation of the SSM.
Our ablative analysis shows that this modification is crucial for the performance of the model, and the method does not work without it.

Unsupervised Keypoint Linear Regression on Face Landmarks:
The standard benchmark of unsupervised keypoint discovery -- the linear regression error in predicting annotated keypoints from the discovered keypoints on faces from the CelebA and MAFL datasets.
The input to the regressor is the keypoint coordinates, and since our method naturally provides uncertainty estimate (the variance of the coordinates) we also experiment with adding the varaince as input features to the regressor).
As can be seen in table below, DLP's performance is state-of-the-art and the full table can be found in the paper.

Method	K (number of unsupervised KP)	Error on MAFL (lower is better)
Zhang (Zhang et al., 2018)	30	3.16
KeyNet (Jakab et al., 2018)	30	2.58
	50	2.54
Ours	25	2.87
	30	2.56
	50	2.43
Ours+ (with variance features)	25	2.52
	30	2.49
	50	2.42

Information from Uncertainty:
We trained DLP with \( K=25 \) particles and used the mean \(\mu \) and the log-variance \( \log(\sigma^2) \) as features for the supervised regression task described above.
As seen in the table above, DLP outperforms KeyNet with \( K=50 \), even though the number of input features to the regressor is the same.
The uncertainty can be further used for model selction and for filtering out low-confidence particles (e.g., filtering bounding boxes of objects), please see the paper for more details.
Particle-based Image Manipulation:
We have implemented a GUI (see interactive demo below) where one can move the particles around and see their effect on the resulting reconstruction. In addition, the features of each particle can be modified to change its appearance (demonstrated on CLEVRER below).

Particle-based Video Prediction:
We present a simple idea for particle-based video prediction -- building a graph from the particles and using a Graph Convolutional Network (GCN) to predict the temporal change of particles. Please see the paper for more details.

Code, pre-trained models and interactive demo are available on GitHub:

[1] Jakab, Tomas, et al. "Unsupervised learning of object landmarks through conditional image generation." Advances in neural information processing systems 31 (2018).
[2] Luke Hawkes - A visual representation of the Chamfer distance function.